客家編碼

提交答案
分數： 100 （部分）
時間限制： 1.0s
記憶體限制： 1G
作者：
電研網管打工人
題目類型

一般而言，普通的編碼每個英文字元都佔一個位元組，即八個位元。在破譯密碼中，我們知道每個字元出現頻率不一、有高有低。假若我們令較少位元代表較常出現的字元，那麼編碼長度就可以縮短惹！！
這實在是太 Hakka 惹吧！！
這種每個字元的編碼長度不一的方法，稱為「變長編碼」。但是，一個字元的編碼不能是另一編碼的前綴 (prefix)。比如如使 'A' 為 \(0\)、 'B' 為 \(1\)、'C' 為 \(01\)，則 \(001\) 可能為 "AAB" 或 "AC"。
為了避免前綴重複，我們可以透過建立特別的二元樹 \(---\) 霍夫曼樹 \(---\) 的方式，以其路徑的左 (\(0\)) 右 (\(1\)) 進行編碼，僅以樹葉（末端節點）為字元，內部節點皆為樹葉的前綴。
現在給你一個字串，請依照各字元出現次數，計算最 Hakka 的編碼長度是多少？？

輸入格式

一字串 \(s\) 長度不超過 \(100000\)、包含非空字元（ASCII 範圍：33~126）。  

輸出格式

請輸出最短編碼長度，單位為位元 (bit)。

範例輸入

aaaaaaaaaaaaaaaabbbbbbbbccccccccddddeeee

範例輸出

88

提示

範例說明

範例輸入中，共有 16 個 'a'、8 個 'b'、8 個 'c'、4 個 'd'、4 個 'e'。
建立霍夫曼樹如下圖：

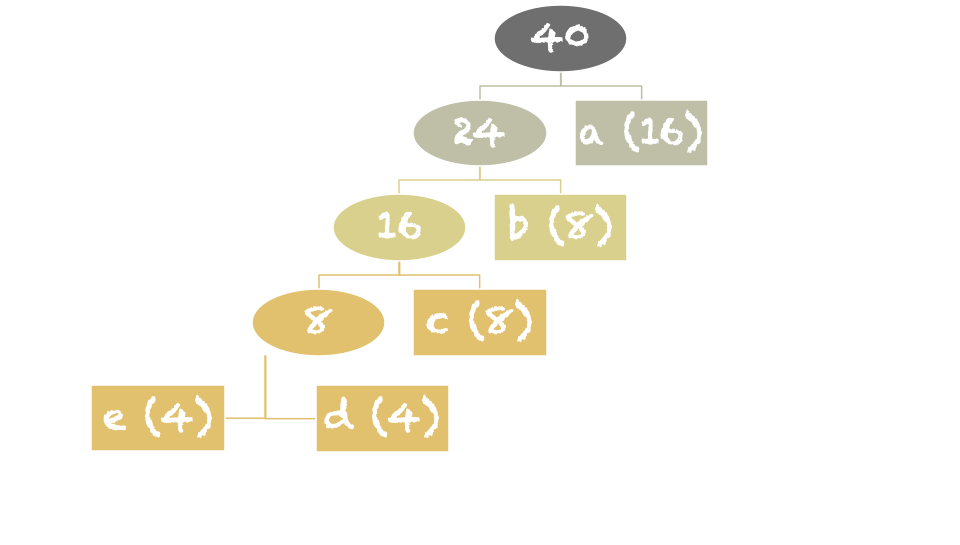
得結果如下表：

字元

a

b

c

d

e

次數

16

8

8

4

4

編碼

1

01

001

0001

0000

故總長度 \(= 16*1 + 8*2 + 8*3 + 4*4 + 4*4 = 88\)。

類題演練

留言

目前沒有評論。