本題簡化自ＵＶＡ８３９，下方會有簡單中文說明！！

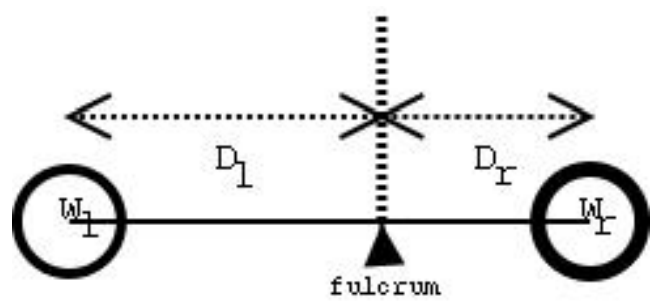
Before being an ubiquous communications gadget, a mobile was just a structure made of strings and wires suspending colourfull things. This kind of mobile is usually found hanging over cradles of small babies.

The figure illustrates a simple mobile. It is just a wire, suspended by a string, with an object on each side. It can also be seen as a kind of lever with the fulcrum on the point where the string ties the wire. From the lever principle we know that to balance a simple mobile the product of the weight of the objects by their distance to the fulcrum must be equal. That is \(W_1 \times D_1 = W_r \times D_r\) where Dl is the left distance, Dr is the right distance, Wl is the left weight and Wr is the right weight.

In a more complex mobile the object may be replaced by a sub-mobile, as shown in the next figure. In this case it is not so straightforward to check if the mobile is balanced so we need you to write a program that, given a description of a mobile as input, checks whether the mobile is in equilibrium or not.

子題說明

對於 20% 測資，天秤只有一個
對於 100% 測資，我也不知道 原出題者沒寫

輸入格式

The input is composed of several lines, each containing 4 integers separated by a single space. The 4 integers represent the distances of each object to the fulcrum and their weights, in the format: \(W_1 \quad D_1 \quad W_r \quad D_r\)

If Wl or Wr is zero then there is a sub-mobile hanging from that end and the following lines define the the sub-mobile. In this case we compute the weight of the sub-mobile as the sum of weights of all its objects, disregarding the weight of the wires and strings. If both Wl and Wr are zero then the following lines define two sub-mobiles: first the left then the right one.

輸出格式

Write YES if the mobile is in equilibrium, write NO otherwise.

範例輸入

0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

範例輸出1

YES

提示

題目說明 這題大概就是給你一個大天秤，兩端可能還掛有其他天秤，問你他們組起來後會不會平衡喇．

每一行輸入有四個整數：左邊重量、左邊力臂、右邊重量、右邊力臂．若重量為０，則代表該側有子天秤．

測資給的順序為遞迴，前序 (Preorder)，即首先是根節點、次而左子樹、最後右子樹．